اتصال (رياضيات)

قالب:عن في الرياضيات، الاتصال هو خاصية طوبولوجية للدالة. في النهج الأول، تكون دالة f متصلة إذا كانت، التغيرات اللانهائية للمتغير x، تقابلها تغيرات لانهائية للقيمة f(x).

يتعلق المثال الأول للدوال المتصلة بالدوال الحقيقية المعرفة على مجال حقيقي والتي يمكن رسم المبيان الخاص بها دون رفع قلم الرصاص. يعطي هذا النهج الأول فكرة عن مفهوم (الدالة لا تقفز) ولكنه لا يكفي لتعريفها، والأهم من ذلك أنه لا يمكن تتبع بعض الرسوم المبيانية للدوال مهما كانت متصلة بهذه الطريقة، على سبيل المثال منحنيات ذات خصائص كسورية مثل دالة كانتور.

تاريخيا عُرَِّف مفهوم الاتصال لدوال ذات متغير حقيقي، حيث عُمِّمَ هذا المفهوم على دوال بين الفضاءات المترية أو بين الفضاءات الطوبولوجة، بشكل خاص وبشكل عام.

وتَبَيَّنَ أن دراسة الدوال المتصلة تكون ناجحة في إيجاد خصائصها (خاصية التقارب، بمعنى أن "قالب:تعبير رياضي"، نظرية القيم الوسطية، نظرية الحدود، التكامل ...).

تعريف الدوال الحقيقية

مثال على دالة متصلة على مجال

مثال على دالة غير متصلة في النقطة 2 :



$\underset{\genfrac{}{}{0ex}{}{x\to 2}{x<2}}{\lim }f(x)=2\ne f(2)$



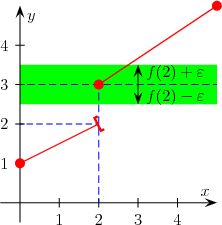
ƒ ليست متصلة على اليسار في 2.



$\underset{\genfrac{}{}{0ex}{}{x\to 2}{x>2}}{\lim }f(x)=3=f(2)$



قالب:تعبير رياضي متصلة على اليمين في 2.

وبالتالي، فإن [[نهاية (رياضيات)|قالب:تعبير رياضي متصلة في قالب:تعبير رياضي إذا وفقط إذا كانت نهاية قالب:تعبير رياضي في قالب:تعبير رياضي موجودة (فهي بالضرورة قالب:تعبير رياضي )]] . (كما في التعريف الرسمي للنهاية، نحصل على تعريف مكافئ عندما نستبدل $|x-a|<\eta$ ب $|x-a|\le \eta$ أو $|f(x)-f(a)|<\epsilon$ ب$|f(x)-f(a)|\le \epsilon$ . )

وهذا يعني أنه إذا أخذنا ε واحد، يمكننا إيجاد مجال يحتوي على قالب:تعبير رياضي بحيث قالب:تعبير رياضي بعيدة بمسافة أقل من ε على قالب:تعبير رياضي.

• إذا كان الاتصال صالح فقط على اليمين (بالنسبة إلى قالب:تعبير رياضي )، نقول أن قالب:تعبير رياضي متصلة على اليمين في قالب:تعبير رياضي . وبنفس الطريقة على اليسار في قالب:تعبير رياضي.
• نقول أن قالب:تعبير رياضي متصلة في قالب:تعبير رياضي عندما تكون متصلة على اليمين وعلى اليسار في قالب:تعبير رياضي
• الدالة قالب:تعبير رياضي متصلة (على قالب:تعبير رياضي) إذا كانت متصلة في كل نقطة قالب:تعبير رياضي من قالب:تعبير رياضي
  الدالة التي تقدم «قفزات» تسمى غير متصلة. يتم توضيح مفهوم القفز على الشكل المقابل، فهو يتوافق مع وجود حد على اليمين وحد على اليسار ليس لكليهما نفس القيمة قالب:تعبير رياضي .

انظر أيضا

• مشتق (رياضيات)
• تشابه الشكل البلوري
• رياضيات التذبذب