مبدأ الطاقة الحرة

قالب:يتيمة مبدأ الطاقة الحرة قالب:إنج هو إطار نظري يُبرز آلية عمل الدماغ في تقليل المفاجأة أو عدم اليقين من خلال بناء تنبؤات تعتمد على نماذج داخلية تُحدّث بناءً على المدخلات الحسية. ويسلط الضوء على هدف الدماغ المتمثل في مواءمة نموذجه الداخلي والعالم الخارجي لتعزيز دقة التنبؤ. يدمج هذا المبدأ الاستدلال البايزي مع الاستدلال النشط، حيث تُوجَّه الأفعال بناءً على التنبؤات وتُنقحها التغذية الراجعة الحسية. و بالتالي سيكون لها تأثيرات واسعة النطاق على فهم وظائف المخ والإدراك و العمل.

ملخص

في الفيزياء الحيوية والعلوم المعرفية، مبدأ الطاقة الحرة هو مبدأ رياضي يصف حسابا رسميًا للقدرات التمثيلية للأنظمة الفيزيائية: أي، و بمعنى بسيط: لماذا تبدو الأشياء الموجودة وكأنها تتبع خصائص الأنظمة التي ترتبط بها.

يثبت أن ديناميكيات الأنظمة الفيزيائية تقلل من كمية الإحتمالية اللوغاريتمية السلبية لبعض النتائج التي تعرف بإسم المفاجأة(surprisal) ؛ أو على نحو مكافئ، الحد الأعلى المتغير لها، والذي يسمى الطاقة الحرة. يتم استخدام المبدأ بشكل خاص في المناهج البايزية لوظائف المخ، ولكن أيضًا في بعض المناهج الخاصة بالذكاء الاصطناعي ؛ وهو مرتبط رسميًا بالطرق البايزية المتغيرة وقد قدمه في الأصل كارل فريستون كتفسير لحلقات الإدراك والفعل المجسدة في علم الأعصاب.

يقوم مبدأ الطاقة الحرة بنمذجة سلوك الأنظمة التي تختلف عن نظام آخر (على سبيل المثال، بيئة التضمين)، ولكنها مقترنة به، حيث تُعرف درجات الحرية التي تنفذ الواجهة بين النظامين بإسم بطانية ماركوفMarkov blanket). بشكل أكثر رسمية، يقول مبدأ الطاقة الحرة أنه إذا كان للنظام قالب:اقتباس مضمن إلى جزيئات، مع بطانيات ماركوف الخاصة بها، فإن مجموعات فرعية من هذا النظام سوف تتبع البنية الإحصائية لمجموعات فرعية أخرى، والتي تعرف بإسم الحالات أو المسارات الداخلية والخارجية للنظام.

يعتمد مبدأ الطاقة الحرة على الفكرة البايزية للدماغ باعتباره قالب:اقتباس مضمن. فبموجب هذا المبدأ، تسعى الأنظمة إلى مسارات أقل إثارة للدهشة، أو على نحو مكافئ، تقلل من الفارق بين التنبؤات القائمة على نموذجها للعالم وإحساسها والإدراك المرتبط بها. فيتم قياس هذا الاختلاف من خلال الطاقة الحرة المتغيرة ويتم التقليل منه عن طريق التصحيح المستمر لنموذج العالم للنظام، أو عن طريق جعل العالم أكثر تشابهًا بتنبؤات النظام. ومن خلال تغيير العالم بشكل نشط لجعله أقرب إلى الحالة المتوقعة، يمكن للأنظمة أيضًا تقليل الطاقة الحرة للنظام. يفترض فريستون أن هذا هو مبدأ كل التفاعلات البيولوجية. ويعتقد فريستون أيضًا أن مبدأه ينطبق على الاضطرابات العقلية و كذلك على الذكاء الاصطناعي. لقد أظهرت تطبيقات الذكاء الاصطناعي القائمة على مبدأ الاستدلال النشط مزايا مقارنة بالطرق الأخرى.

مبدأ الطاقة الحرة هو مبدأ رياضي في فيزياء المعلومات: يشبه إلى حد كبير مبدأ الحد الأقصى للإنتروبيا أو مبدأ أقل فعل، وهو صحيح على أسس رياضية. لذلك، إن أي محاولة لدحضه هي خطأ تصنيفي، تشبه محاولة دحض حساب التفاضل والتكامل من خلال إجراء ملاحظات تجريبية. ببساطة لا يمكن إبطال نظرية رياضية بهذه الطريقة؛ و بدلاً من ذلك، سيحتاج المرء إلى استنباط تناقض رسمي من النظرية. في مقابلة أجريت عام 2018، أوضح فريستون ما يستلزمه عدم خضوع مبدأ الطاقة الحرة للدحض : قالب:اقتباس مضمن وهناك العديد من الأمثلة على هذه الفرضيات المدعومة بأدلة تجريبية.

الخلفية

إن فكرة أن الأنظمة البيولوجية المنظمة ذاتيًا - مثل الخلية أو الدماغ - يمكن فهمها على أنها تقلل من الطاقة الحرة المتغيرة تستند إلى عمل هلمهولتز في الاستدلال اللاواعي و العلاجات اللاحقة في علم النفس و التعلم الآلي. الطاقة الحرة المتغيرة هي دالة للملاحظات وكثافة الاحتمالية على أسبابها الخفية. يتم تعريف هذه الكثافة المتغيرة فيما يتعلق بنموذج احتمالي يولد ملاحظات متوقعة من أسباب مفترضة. في هذا الإطار، توفر الطاقة الحرة تقريبًا لدليل النموذج البايزي. لذلك، يمكن اعتبار تقليله بمثابة عملية استدلال بايزية. فعندما يقوم نظام ما بإجراء ملاحظات نشطة لتقليل الطاقة الحرة، فإنه يقوم ضمناً بالاستدلال النشط و يعظم أدلة نموذجه للعالم.

ومع ذلك، فإن الطاقة الحرة تشكل أيضًا حدًا أعلى لنتائج المعلومات الذاتية، حيث يكون متوسط المفاجأة على المدى الطويل هو تغير الإنتروبية(entropy). و هذا يعني أنه إذا عمل النظام على تقليل الطاقة الحرة، فإنه سيضع ضمنياً أعلى حد لإنتروبيا النتائج - أو الحالات الحسية - التي تقوم بأخذ عينات منها.

العلاقة مع النظريات الأخرى

الاستدلال النشط وثيق الصلة بنظرية المنظم الجيدgood) regulator theorem) و الحسابات ذات الصلة بالتنظيم الذاتي، مثل التجميع الذاتي، و تكوين الأنماط، و التكوين الذاتي و التكوين العملي. فهو بذلك يتناول الموضوعات التي تمت مناقشتها في علم التحكم الآلي، و سينيرجيتيك(synergetics) و الإدراك المجسد. نظرًا لأنه يمكن التعبير عن الطاقة الحرة باعتبارها الطاقة المتوقعة للملاحظات تحت كثافة التباين مطروحًا منها إنتروبيتها، فإنها ترتبط أيضًا بمبدأ الحد الأقصى للإنتروبيا. و أخيرًا، نظرًا لأن متوسط الزمن للطاقة هو الفعل، فإن مبدأ الحد الأدنى للطاقة الحرة المتغيرة هو مبدأ الحد الأدنى للفعل. لقد طبق الاستدلال النشط الذي يسمح بثبات المقياس على نظريات و مجالات أخرى أيضًا. على سبيل المثال، تم تطبيقه على علم الاجتماع، واللغويات والاتصال، وعلم العلامات، و علم الأوبئة و غيرها.

الطاقة الحرة السلبية تعادل رسميًا الحد الأدنى للأدلة، والذي يستخدم عادةً في التعلم الآلي لتدريب النماذج التوليدية، مثل المشفرات التلقائية المتغيرة.

الفعل و الإدراك

الشكل 1: توضح هذه المخططات تقسيم الحالات إلى حالات داخلية$\mu (t)$ والحالات الخارجية (المخفية، الكامنة)$\psi (t)$ التي يتم فصلها بواسطة بطانية ماركوف - والتي تتألف من حالات حسية$s(t)$ والدول النشطة$a(t)$. تُظهر اللوحة العلوية نفس التبعيات تمامًا ولكن مع إعادة ترتيبها بحيث ترتبط الحالات الداخلية بالحالات داخل الخلايا، بينما تصبح الحالات الحسية هي الحالات السطحية للغشاء الخلوي الذي يغطي الحالات النشطة (على سبيل المثال، خيوط الأكتين في الهيكل الخلوي). تُظهر اللوحة السفلية هذا التقسيم كما سيتم تطبيقه على الفعل والإدراك في الدماغ؛ حيث تعمل الحالات النشطة والداخلية على تقليل الطاقة الحرة الوظيفية للحالات الحسية. إن التنظيم الذاتي اللاحق للحالات الداخلية يتوافق بعد ذلك مع الإدراك، في حين يربط الفعل حالات الدماغ بالحالات الخارجية.

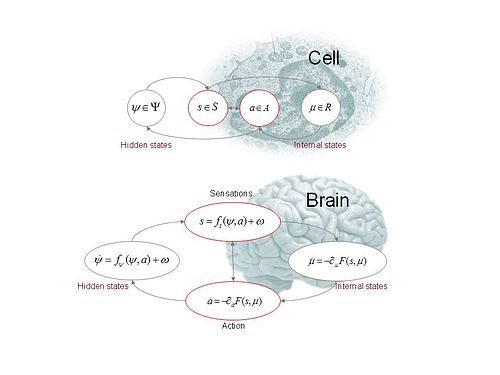
يطبق الاستدلال النشط تقنيات الاستدلال البايزي التقريبي لاستنتاج أسباب البيانات الحسية من نموذج "توليدي" لكيفية حدوث هذه البيانات،ثم استخدام هذه الاستدلالات لتوجيه العمل. تتميز قاعدة بايز بوصف الانعكاس الأمثل احتماليًا لمثل هذا النموذج السببي، ولكن تطبيقها عادة ما يكون صعبًا حسابيًا، مما يؤدي إلى استخدام أساليب تقريبية بالمقابل. في الاستدلال النشط، فإن الفئة الرائدة من هذه الأساليب التقريبية هي الأساليب المتغيرة، لأسباب عملية ونظرية: عملية، لأنها غالبًا ما تؤدي إلى إجراءات استدلال بسيطة ونظرية، لأنها مرتبطة بالمبادئ الفيزيائية الأساسية، كما تمت مناقشته أعلاه.

تعمل طرق التباين هذه على تقليل الحد الأعلى للتباعد بين الاستدلال الأمثل لبايز (أو " اللاحق ") وتقريبه وفقًا للطريقة. ويُعرف هذا الحد الأعلى بالطاقة الحرة، وبالتالي يمكننا وصف الإدراك بأنه تقليل الطاقة الحرة فيما يتعلق بالمعلومات الحسية الواردة، والفعل بأنه تقليل نفس الطاقة الحرة فيما يتعلق بمعلومات الفعل الصادرة. إن هذا التحسين الثنائي الشامل هو سمة من سمات الاستدلال النشط، و مبدأ الطاقة الحرة هو الفرضية التي مفادها أن جميع الأنظمة التي تدرك و تتصرف يمكن وصفها بهذه الطريقة.

من أجل توضيح آليات الاستدلال النشط عبر مبدأ الطاقة الحرة، يجب تحديد نموذج توليدي، وهذا يتضمن عادةً مجموعة من وظائف كثافة الاحتمالية التي تميز معًا النموذج السببي. ومن بين هذه المواصفات ما يلي. تم تصميم النظام على أنه يسكن مساحة الدولة$X$، بمعنى أن حالاتها تشكل نقاط هذا الفضاء. ثم يتم تقسيم مساحة الحالة إلى عوامل وفقًا لـ$X=\mathrm{\Psi }\times S\times A\times R$، أين$\mathrm{\Psi }$ هي مساحة الحالات "الخارجية" التي "تختفي" عن الفاعل (بمعنى عدم إدراكها أو الوصول إليها بشكل مباشر)،$S$ هي مساحة الحالات الحسية التي يدركها العامل مباشرة،$A$ هي مساحة أفعال الوكيل الممكنة، و$R$ هي مساحة من الحالات "الداخلية" الخاصة بالوكيل.

بالتوافق مع الشكل 1، لاحظ أنه في ما يلي$\dot{\psi },\psi ,s,a$ و$\mu$ هي وظائف للزمن (المستمر)$t$. النموذج التوليدي هو تحديد لوظائف الكثافة التالية:

• نموذج حسي،$p_S:S\times \mathrm{\Psi }\times A\to ℝ$، غالبًا ما يتم كتابتها على هذا النحو$p_S(s\mid \psi ,a)$، تحديد احتمالية البيانات الحسية المقدمة للحالات و الأفعال الخارجية؛
• نموذج عشوائي للديناميكيات البيئية،$p_{\mathrm{\Psi }}:\mathrm{\Psi }\times \mathrm{\Psi }\times A\to ℝ$، مكتوبة في كثير من الأحيان$p_{\mathrm{\Psi }}(\dot{\psi }\mid \psi ,a)$، التي تصف كيف يتوقع العامل أن تتطور الحالات الخارجية بمرور الوقت$t$، بالنظر إلى تصرفات الوكيل؛
• نموذج عمل$p_A:A\times R\times S\to ℝ$, مكتوبة$p_A(a\mid \mu ,s)$، ووصف كيفية اعتماد أفعال الوكيل على حالاته الداخلية وبياناته الحسية؛ و
• نموذج داخلي،$p_R:R\times S\to ℝ$, مكتوبة$p_R(\mu \mid s)$، والتي تصف كيف تعتمد الحالات الداخلية للوكيل على بياناته الحسية.

تحدد وظائف الكثافة هذه عوامل " النموذج المشترك "، الذي يمثل المواصفات الكاملة للنموذج التوليدي، والذي يمكن كتابته على النحو التالي:

$p_{\text{Bayes}}(\dot{\psi },s,a,\mu \mid \psi )=p_S(s\mid \psi ,a)p_{\mathrm{\Psi }}(\dot{\psi }\mid \psi ,a)p_A(a\mid \mu ,s)p_R(\mu \mid s)$.

ثم تحدد قاعدة بايز "الكثافة الخلفية"$p(\dot{\psi }|s,a,\mu ,\psi )$، و التي تعبر عن اعتقاد مثالي احتماليًا بشأن الحالة الخارجية$\psi$ بالنظر إلى الحالة السابقة و أفعال الوكيل و الإشارات الحسية و الحالات الداخلية. منذ الحوسبة$p_{\text{Bayes}}$ من الصعب حسابيًا حل هذه المشكلة، حيث يؤكد مبدأ الطاقة الحرة وجود "كثافة متغيرة"$q(\dot{\psi }|s,a,\mu ,\psi )$، أين$q$ هو تقريب ل$p_{\text{Bayes}}$. ومن ثم يتم تعريف الطاقة الحرة على أنها

$\begin{array}{cc}\underset{\mathrm{f}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{-}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y}}{\underbrace{F(\mu ,a;s)}}& =\underset{\text{expected energy}}{\underbrace{{𝔼}_{q(\dot{\psi })}[-\log p(\dot{\psi },s,a,\mu \mid \psi )]}}-\underset{\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{y}}{\underbrace{ℍ[q(\dot{\psi }\mid s,a,\mu ,\psi )]}}\\ & =\underset{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}{\underbrace{-\log p(s)}}+\underset{\mathrm{d}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}}{\underbrace{𝕂𝕃[q(\dot{\psi }\mid s,a,\mu ,\psi )\parallel p_{\text{Bayes}}(\dot{\psi }\mid s,a,\mu ,\psi )]}}\\ & \ge \underset{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}{\underbrace{-\log p(s)}}\end{array}$

و يحدد الفعل و الإدراك باعتبارهما مشكلة التحسين المشتركة

$\begin{array}{cc}{\mu }^{*}& =\underset{\mu }{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\{F(\mu ,a;s))\}\\ a^{*}& =\underset{a}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\{F({\mu }^{*},a;s)\}\end{array}$

حيث الدول الداخلية$\mu$ يتم استخدامها عادةً لترميز معلمات الكثافة "المتغيرة"$q$ ومن ثم فإن "أفضل تخمين" للوكيل فيما يتعلق بالاعتقاد اللاحق$\mathrm{\Psi }$. لاحظ أن الطاقة الحرة هي أيضًا حد أعلى لمقياس المفاجأة الحسية ( الهامشية أو المتوسطة) للعامل، وبالتالي فإن تقليل الطاقة الحرة غالبًا ما يكون مدفوعًا بتقليل المفاجأة.

تقليل الطاقة المجانية

تقليل استهلاك الطاقة المجانية و التنظيم الذاتي

أُقترح تقليل الطاقة الحرة باعتبارها السمة المميزة للأنظمة ذاتية التنظيم عندما يتم صياغتها كأنظمة ديناميكية عشوائية. تعتمد هذه الصيغة على بطانية ماركوف (تتكون من حالات الفعل و الحواس) التي تفصل بين الحالات الداخلية و الخارجية. فإذا كانت الحالات الداخلية والفعل تعمل على تقليل الطاقة الحرة، فإنها تضع حدًا أعلى على إنتروبيا الحالات.

$\underset{T\to \mathrm{\infty }}{\lim }\frac{1}{T}\underset{\text{free-action}}{\underbrace{\underset{0}{\overset{T}{\int }}F(s(t),\mu (t))dt}}\ge \underset{T\to \mathrm{\infty }}{\lim }\frac{1}{T}\underset{0}{\overset{T}{\int }}\underset{\text{surprise}}{\underbrace{-\log p(s(t)\mid m)}}dt=H[p(s\mid m)]$

و يرجع ذلك إلى أن المتوسط الطويل الأمد للمفاجأة هو الإنتروبيا ـ وفقاً للافتراضات الإرجوديكية(ergodic). تقاوم هذه الحدود الميل الطبيعي إلى الفوضى - من النوع المرتبط بالقانون الثاني للديناميكا الحرارية ونظرية التقلب(fluctuation theorem). و مع ذلك، فإن صياغة مبدأ موحد للعلوم الحيوية من حيث المفاهيم المستمدة من الفيزياء الإحصائية، مثل النظام الديناميكي العشوائي، و الحالة الثابتة غير المتوازنة، و الديناميكية، يفرض قيودًا كبيرة على الدراسة النظرية و التجريبية للأنظمة البيولوجية مع خطر إخفاء جميع الميزات التي تجعل الأنظمة البيولوجية أنواعًا مثيرة للاهتمام من الأنظمة ذاتية التنظيم.

تقليل الطاقة الحرة و الاستدلال البايزي

يمكن صياغة جميع الاستدلالات البايزية من حيث تقليل الطاقة الحرة</link>. عندما يتم تقليل الطاقة الحرة فيما يتعلق بالحالات الداخلية، يتم تقليل تباعد كولباك-ليبلر بين الكثافة المتغيرة والخلفية على الحالات المخفية. يتوافق هذا مع الاستدلال البايزي التقريبي - عندما يكون شكل الكثافة المتغيرة ثابتًا - واد الاستدلال البايزي الدقيق بخلاف ذلك. لذلك يوفر تقليل الطاقة الحرة وصفًا عامًا للاستدلال و الترشيح البايزي (على سبيل المثال، ترشيح كالمانKalman filtering ). يتم استخدامه أيضًا في اختيار النموذج البايزي، حيث يمكن العمل على تحلل الطاقة الحرة بشكل مفيد إلى التعقيد و الدقة:

$\underset{\text{free-energy}}{\underbrace{F(s,\mu )}}=\underset{\text{complexity}}{\underbrace{D_{\mathrm{K}\mathrm{L}}[q(\psi \mid \mu )\parallel p(\psi \mid m)]}}-\underset{\mathrm{a}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}}{\underbrace{E_q[\log p(s\mid \psi ,m)]}}$

توفر النماذج ذات الحد الأدنى من الطاقة الحرة شرحًا دقيقًا للبيانات، في ظل تكاليف التعقيد (راجع شفرة أوكام و المعالجات الأكثر رسمية للتكاليف الحسابية ). هنا، التعقيد هو التباعد بين الكثافة المتغيرة والمعتقدات السابقة حول الحالات المخفية (أي درجات الحرية الفعالة المستخدمة لشرح البيانات).

تقليل الطاقة الحرة والديناميكا الحرارية

الطاقة الحرة المتغيرة هي دالة نظرية معلوماتية وهي مختلفة عن الطاقة الحرة الديناميكية الحرارية (هيلمهولتز). ومع ذلك، فإن مصطلح التعقيد للطاقة الحرة المتغيرة يشترك في نفس النقطة الثابتة مثل طاقة هلمهولتز الحرة (تحت افتراض أن النظام مغلق ترموديناميكيًا ولكن ليس معزولًا). ويرجع ذلك إلى أن تعليق الاضطرابات الحسية (لفترة زمنية طويلة مناسبة) يؤدي إلى تقليل التعقيد (لأن الدقة يمكن إهمالها). في هذه المرحلة، يكون النظام في حالة توازن و تقلل الحالات الداخلية من طاقة هلمهولتز الحرة، وفقًا لمبدأ الحد الأدنى للطاقة.

التقليل من الطاقة الحرة و نظرية المعلومات

إن تقليل الطاقة الحرة يعادل تعظيم المعلومات المتبادلة بين الحالات الحسية والحالات الداخلية التي تحدد كثافة التباين (لكثافة التباين الثابتة للإنتروبيا). يرتبط هذا بتقليل الطاقة المجانية إلى الحد الأدنى من التكرار.

تقليل الطاقة المجانية في علم الأعصاب

يوفر تقليل الطاقة الحرة طريقة مفيدة لصياغة نماذج معيارية (Bayes optimal) للاستدلال العصبي و التعلم في ظل عدم اليقين وبالتالي فهو يشترك في فرضية الدماغ البايزية. تعتمد العمليات العصبية التي يتم وصفها من خلال تقليل الطاقة الحرة على طبيعة الحالات المخفية:$\mathrm{\Psi }=X\times \mathrm{\Theta }\times \mathrm{\Pi }$ والتي يمكن أن تشمل متغيرات تعتمد على الوقت، ومعلمات ثابتة للوقت ودقة (التباين العكسي أو درجة الحرارة) للتقلبات العشوائية. تتوافق عملية تقليل المتغيرات والمعلمات والدقة مع الاستدلال والتعلم وترميز عدم اليقين على التوالي.

الاستدلال الإدراكي و التصنيف

يقوم تقليل الطاقة الحرة بإضفاء الطابع الرسمي على مفهوم الاستدلال اللاواعي في الإدراك و يوفر نظرية معيارية (بيزية) للمعالجة العصبية. تعتمد نظرية العملية المرتبطة بديناميكيات الخلايا العصبية على تقليل الطاقة الحرة من خلال الانحدار التدريجي. يتوافق هذا مع الترشيح البايزي المعمم (حيث يشير ~ إلى متغير في إحداثيات الحركة المعممة و$D$ هو عامل مصفوفة مشتقة):

$\dot{\tilde{\mu }}=D\tilde{\mu }-{\partial }_{\mu }F(s,\mu ){|}_{\mu =\tilde{\mu }}$

عادةً ما تكون النماذج التوليدية التي تحدد الطاقة الحرة غير خطية وتسلسلية (مثل التسلسلات الهرمية القشرية في الدماغ). تتضمن الحالات الخاصة للتصفية المعممة تصفية كالمان، والتي تعادل رسميًا الترميز التنبئي( predictive coding وهو استعارة شائعة لتمرير الرسائل في الدماغ. في ظل النماذج الهرمية، يتضمن الترميز التنبئي التبادل المتكرر لأخطاء التنبؤ الصاعدة (من أسفل إلى أعلى) والتنبؤات الهابطة (من أعلى إلى أسفل) بما يتوافق مع تشريح وعلم وظائف الأعضاء الحسية والأنظمة الحركية.

التعلم الإدراكي و الذاكرة

في الترميز التنبئي، يؤدي تحسين معلمات النموذج من خلال الانحدار التدريجي على التكامل الزمني للطاقة الحرة (الفعل الحر) إلى تقليل اللدونة الترابطية أو اللدونة الهيبية و يرتبط باللدونة المشبكية في الدماغ.

الدقة الإدراكية و الانتباه والإبراز

يتوافق تحسين معلمات الدقة مع تحسين مكسب أخطاء التنبؤ (راجع مكسب كالمان). في التنفيذات العصبية المعقولة للترميز التنبئي، يتوافق هذا مع تحسين قابلية إثارة الخلايا الهرمية السطحية وقد تم تفسيره من حيث اكتساب الانتباه.

محاكاة النتائج التي تم التوصل إليها من مهمة الانتباه الانتقائي التي تم تنفيذها من خلال إعادة صياغة بايزية لـ SAIM بعنوان PE-SAIM في بيئة الكائنات المتعددة. تظهر الرسوم البيانية المسار الزمني لتنشيط FOA ووحدتي القالب في شبكة المعرفة.

وفيما يتعلق بالجدال حول من أعلى إلى أسفل مقابل من أسفل إلى أعلى، والذي تمت معالجته باعتباره مشكلة مفتوحة رئيسية تتعلق بالانتباه، فقد نجح نموذج حسابي في توضيح الطبيعة الدائرية للتفاعل بين الآليات من أعلى إلى أسفل ومن أسفل إلى أعلى. وباستخدام نموذج ناشئ راسخ للانتباه، وهو سايم( SAIM)، اقترح المؤلفون نموذجًا يسمى بي سايم(PE-SAIM)، والذي، على النقيض من الإصدار القياسي، يقترب من الانتباه الانتقائي من موقف من أعلى إلى أسفل. يأخذ النموذج في الاعتبار انتقال أخطاء التنبؤ إلى نفس المستوى أو مستوى أعلى، من أجل تقليل دالة الطاقة التي تشير إلى الفرق بين البيانات و سببها، أو بعبارة أخرى، بين النموذج التوليدي واللاحق. و لزيادة صحة النتائج، قاموا أيضًا بدمج المنافسة العصبية بين المحفزات في نموذجهم. الميزة البارزة لهذا النموذج هي إعادة صياغة دالة الطاقة الحرة فقط من حيث أخطاء التنبؤ أثناء أداء المهمة:

$\frac{\partial E^{total}(Y^{VP},X^{SN},x^{CN},y^{KN})}{\partial y_{mn}^{SN}}=x_{mn}^{CN}-b^{CN}{\epsilon }_{nm}^{CN}+b^{CN}\sum _k({\epsilon }_{knm}^{KN})$

أين$E^{total}$ هي دالة الطاقة الكلية للشبكات العصبية التي تستلزمها، و${\epsilon }_{knm}^{KN}$ هو خطأ التنبؤ بين النموذج التوليدي (السابق) والتغيير اللاحق بمرور الوقت. يكشف مقارنة النموذجين عن تشابه ملحوظ بين نتائجهما الخاصة مع تسليط الضوء أيضًا على تناقض ملحوظ، حيث يركز النموذج في الإصدار القياسي من SAIM بشكل أساسي على الاتصالات المثيرة، بينما في PE-SAIM، يتم الاستفادة من الاتصالات المثبطة للتوصل إلى استنتاج. وقد ثبت أيضًا أن النموذج مناسب للتنبؤ ببيانات تخطيط كهربية الدماغ والتصوير بالرنين المغناطيسي الوظيفي المستمدة من التجارب البشرية بدقة عالية. على نفس المنوال، طبق يحيى وآخرون أيضًا مبدأ الطاقة الحرة لاقتراح نموذج حسابي لمطابقة القالب في الانتباه البصري الانتقائي الخفي الذي يعتمد في الغالب على SAIM. وفقًا لهذه الدراسة، يتم الوصول إلى إجمالي الطاقة الحرة لكامل مساحة الحالة عن طريق إدخال إشارات من أعلى إلى أسفل في الشبكات العصبية الأصلية، وبالتالي نستنتج نظامًا ديناميكيًا يشتمل على خطأ التنبؤ بالتغذية الأمامية والخلفية.

الاستدلال النشط

عندما يتم تطبيق الانحدار المتدرج على الإجراء$\dot{a}=-{\partial }_{a}F(s,\tilde{\mu })$ يمكن فهم التحكم الحركي من حيث الأقواس الانعكاسية الكلاسيكية التي تشارك في التنبؤات الهابطة (القشرية الشوكية). وهذا يوفر صيغة تعمم حل نقطة التوازن - لمشكلة درجات الحريةthe( degrees of freedom problem) - على مسارات الحركة.

الاستدلال النشط و التحكم الأمثل

يرتبط الاستدلال النشط بالتحكم الأمثل من خلال استبدال وظائف القيمة أو التكلفة بالاعتقادات السابقة حول انتقالات الحالة أو التدفق. يستغل هذا الارتباط الوثيق بين الترشيح البايزي وحل معادلة بيلمان. ومع ذلك، فإن الاستدلال النشط يبدأ بـ (الأسبقيات) التدفق$f=\mathrm{\Gamma }\cdot \mathrm{\nabla }V+\mathrm{\nabla }\times W$ التي تم تحديدها باستخدام مقياس$V(x)$ وناقل$W(x)$ وظائف القيمة لمساحة الحالة (راجع تحلل هلمهولتز ). هنا،$\mathrm{\Gamma }$ هي سعة التقلبات العشوائية والتكلفة هي$c(x)=f\cdot \mathrm{\nabla }V+\mathrm{\nabla }\cdot \mathrm{\Gamma }\cdot V$. الأسبقيات على التدفق$p(\tilde{x}\mid m)$ إحداث حالة سابقة على الحالات$p(x\mid m)=\exp (V(x))$ هذا هو الحل لمعادلات كولموغوروف الأمامية المناسبة. على النقيض من ذلك، يعمل التحكم الأمثل على تحسين التدفق، مع الأخذ في الاعتبار دالة التكلفة، على افتراض أن$W=0$ (أي أن التدفق خالي من التجعيد أو يتمتع بتوازن تفصيلي). عادةً، يستلزم هذا حل معادلات كولموغوروف العكسية.

الاستدلال النشط و نظرية القرار الأمثل (اللعبة)

يتم التعامل مع مشاكل القرار الأمثل (والتي عادة ما يتم صياغتها على أنها عمليات قرار ماركوف قابلة للملاحظة جزئيًا ) ضمن الاستدلال النشط عن طريق استيعاب وظائف المنفعة في المعتقدات السابقة. في هذا الإطار، فإن الدول التي تتمتع بمنفعة عالية (تكلفة منخفضة) هي الدول التي يتوقع الوكيل أن يشغلها. من خلال تجهيز النموذج التوليدي بحالات مخفية تعمل على نمذجة التحكم، فإن السياسات (تسلسلات التحكم) التي تقلل من الطاقة الحرة المتغيرة تؤدي إلى حالات فائدة عالية.

في علم الأعصاب، يُعتقد أن منظمات الأعصاب مثل الدوبامين تعمل على الإبلاغ عن دقة أخطاء التنبؤ من خلال تعديل مكسب الخلايا الرئيسية التي تشفر خطأ التنبؤ. فيرتبط هذا ارتباطًا وثيقًا بدور الدوبامين في الإبلاغ عن أخطاء التنبؤ في حد ذاتها والحسابات الحسابية ذات الصلة - ولكنه يختلف رسميًا عن ذلك.

الاستدلال النشط وعلم الأعصاب الإدراكي

تم استخدام الاستدلال النشط لمعالجة مجموعة من القضايا في علم الأعصاب الإدراكي ووظائف المخ والطب النفسي العصبي، بما في ذلك ملاحظة الفعل، الخلايا العصبية المرآتيةmirror) neurons)، حركات العين السريعة والبحث البصري، حركات العين، النوم، الأوهام، الانتباه، اختيار الفعل، الوعي، الهستيريا والذهان. غالبًا ما تعتمد تفسيرات الفعل في الاستدلال النشط على فكرة أن الدماغ لديه "تنبؤات عنيدة" لا يمكنه تحديثها، مما يؤدي إلى أفعال تجعل هذه التنبؤات تتحقق.

روابط خارجية

• العلوم السلوكية وعلوم الدماغ (بقلم آندي كلارك)