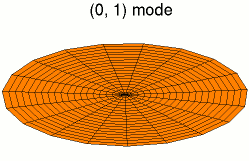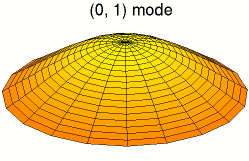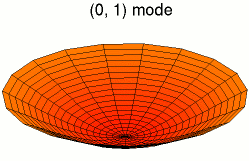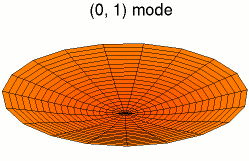
function main()
k = 0; % k-th asimuthal number and bessel function
p = 1; % p-th bessel root
q=find_pth_bessel_root(k, p);
N=20; % used for plotting
% Get a grid
R1=linspace(0.0, 1.0, N);
Theta1=linspace(0.0, 2*pi, N);
[R, Theta]=meshgrid(R1, Theta1);
X=R.*cos(Theta);
Y=R.*sin(Theta);
T=linspace(0.0, 2*pi/q, N); T=T(1:(N-1));
for iter=1:length(T);
t = T(iter);
Z=sin(q*t)*besselj(k, q*R).*cos(k*Theta);
figure(1); clf;
surf(X, Y, Z);
caxis([-1, 1]);
shading faceted;
colormap autumn;
% viewing angle
view(108, 42);
axis([-1, 1, -1, 1, -1, 1]);
axis off;
H=text(0, -0.3, 1.4, sprintf('(%d, %d) mode', k, p), 'fontsize', 25);
file=sprintf('Frame%d.png', 1000+iter);
disp(sprintf('Saving to %s', file));
print('-dpng', '-zbuffer', '-r100', file);
pause(0.1);
end
% converted to gif with the command
% convert -antialias -loop 10000 -delay 10 -scale 50% Frame10* Drum_vibration_mode01.gif
function r = find_pth_bessel_root(k, p)
% a dummy way of finding the root, just get a small interval where the root is
X=0.5:0.5:(10*p+1); Y = besselj(k, X);
[a, b] = find_nthroot(X, Y, p);
X=a:0.01:b; Y = besselj(k, X);
[a, b] = find_nthroot(X, Y, 1);
X=a:0.0001:b; Y = besselj(k, X);
[a, b] = find_nthroot(X, Y, 1);
r=(a+b)/2;
function [a, b] = find_nthroot(X, Y, n)
l=0;
m=length(X);
for i=1:(m-1)
if ( Y(i) >= 0 & Y(i+1) <= 0 ) | ( Y(i) <= 0 & Y(i+1) >= 0 )
l=l+1;
end
if l==n
a=X(i); b=X(i+1);
%disp(sprintf('Error in finding the root %0.9g', b-a));
return;
end
end
disp('Root not found!');