متعدد اللوغاريتمات

في الرياضيات، يعد متعدد اللوغاريتمات قالب:إنج، المعروف أيضًا باسم دالة جونكيير نسبة لألفريد جونكيير (Alfred Jonquière)، دالة خاصة قالب:تعبير رياضي من الرتبة قالب:Mvar والمدخل قالب:Mvar. فقط للقيم الخاصة لـ قالب:Mvar ، يُخْتَزَلْ متعدد اللوغاريتمات إلى دالة ابتدائية مثل اللوغاريتم الطبيعي أو دالة كسرية. في الإحصاء الكمي، تظهر دالة متعدد اللوغاريتمات على أنها الشكل المغلق لتكاملات توزيع فيرمي-ديراك وتوزيع بوز-آينشتاين، وتُعرف أيضًا باسم تكامل فيرمي-ديراك أو تكامل بوز-آينشتاين على الترتيب. في الكهروديناميكا الكمية، يظهر متعدد اللوغاريتمات من الرتبة الطبيعية العدد في حساب العمليات التي تمثلها مخططات فاينمان عالية الرتبة.

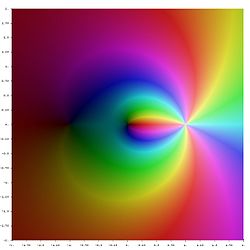
• دوال متعدد اللوغاريتمات في المستوي المركب
• 
  قالب:تعبير رياضي
• 
  قالب:تعبير رياضي
• 
  قالب:تعبير رياضي
• 
  قالب:تعبير رياضي
• 
  قالب:تعبير رياضي
• 
  قالب:تعبير رياضي
• 
  قالب:تعبير رياضي

تُعرَّف دالة متعدد اللوغاريتمات بمتسلسلة القوى بدلالة قالب:Mvar، وهي أيضًا متسلسلة دركليه بدلالة قالب:Mvar:

${\mathrm{Li}}_s(z)=\sum _{k=1}^{\mathrm{\infty }}\frac{z^k}{k^s}=z+\frac{z^2}{2^s}+\frac{z^3}{3^s}+\cdots$

هذا التعريف صالح للرتبة المركبة الاختيارية قالب:Mvar ولجميع المداخل المركبة قالب:Mvar ذات قالب:تعبير رياضي؛ يمكن أن يمتد إلى قالب:تعبير رياضي من خلال عملية الامتداد التحليلي. (هنا يُفهم المقام قالب:Mvar على أنه قالب:تعبير رياضي). تتضمن الحالة الخاصة قالب:تعبير رياضي اللوغاريتم الطبيعي العادي، قالب:تعبير رياضي، بينما تسمى الحالات الخاصة قالب:تعبير رياضي و قالب:تعبير رياضي ثنائي اللوغاريتم (Dilogarithm) (يشار إليه أيضًا باسم دالة سبنس Spence) و ثلاثي اللوغاريتمات (Trilogarithm) على الترتيب. يأتي اسم الدالة من حقيقة أنه يمكن تعريفها أيضًا على أنها تكامل متكرر لنفسها:

${\mathrm{Li}}_{s+1}(z)=\underset{0}{\overset{z}{\int }}\frac{{\mathrm{Li}}_s(t)}{t}dt$

وبالتالي فإن متعدد اللوغاريتمات هو تكامل دالة تتضمن اللوغاريتم، وما إلى ذلك. بالنسبة للرتب الصحيحة السالبة قالب:Mvar، فإن متعدد اللوغاريتمات هو دالة كسرية.