سطح مكافئي

سطح مكافئي زائدي

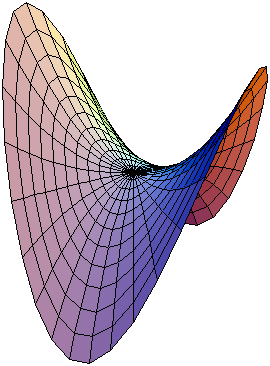
في الرياضيات السطح المكافئي أو المجسم المكافئي قالب:إنج هو أحد السطوح التربيعية ثلاثية الأبعاد والذي يكون معادلته كالتالي:

${\left(\frac{x}{a}\right)}^2+{\left(\frac{y}{b}\right)}^2+2z=0$ (للسطح المكافئي الإهليلجي)

أو

${\left(\frac{x}{a}\right)}^2-{\left(\frac{y}{b}\right)}^2+2z=0$ (للسطح المكافئي الزائدي)

هناك نوعان من الأسطح المكافئية: الإهليلجية والزائدية. الإهليلجية يكون شكلها ككوب ويمكن أن يكون لها نقطة قيم صغرى أو كبرى. أما الزائدية فيكون شكلها كشكل سرج الحصان ولها نقطة حرجة يطلق عليها مسمى النقطة السرجية، تعد الأسطح الزائدية أسطحا مسطرة.

في حالة a تساوي b في المعادلة الأولى يسمى الشكل الناتج سطحا مكافئيا دورانيا وهو الشكل الذي ينتج من دوران قطع مكافئي حول محوره. يستخدم الشكل لتكوين بعض المرايا أو الأطباق اللاقطة. يسمى الشكل أيضا بالسطح المكافئي الدائري.

هندسة العمارة

من بين الامثلة للقباب بسطح مكافئ اهليجي، القبة التي بناها المهندس جيانبيرو كاستيلوتشي في الفترة : 1978-1980. والتي تغطي صالة كبيرة متعددة الأغراض للأنشطة الرياضية، مصممة لاستيعاب 2000 شخص جالس.

السطح المكافئي، في الهندسة الوصفية, يشير إلى سطح ثنائي ذو راسم مكافئي، والذي وفقا لنوع دالته المخروطية (قطع ناقص، مكافئ أو زائد), يمكن ان يكون بالتوالي مكافئ إهليلجي (انظر المثال المرفق) أو مكافئي أو مكافئي زائدي.

معرض صور

• 
  سطح مكافئي إهليلجي
• 
  سطح مكافئي زائدي ويمكن تسميته أيضا زائد مكافئي لان الراسم (generatrix) يمكن ان يكون دالة (Directrix) والعكس صحيح
• 
  نمذجة هيكل القطع المكافئي في موضع عام - التحقق من الحلزونات القطرية
• 
  تغيير الهيكل الأساسي لسطح مكافئي إهليلجي حول محور لا ينتمي إلى أي من مستويي التماثل
• 
  صورة لمخروط متماس لسطح مكافئي دوراني، حيث تنتمي قمة المخروط إلى واحد من مستويين التماثل للسطح
• 
  تحويل إسقاطي بين نظامين قطبيين بالنسبة لسطح تربيعي، في هذه الحالة سطح مكافئي إهليلجي
• 
  تحويل إسقاطي بين نظم قطبية بالنسبة لسطح مكافئي إهليلجي
• 
  تحويل إسقاطي على سطح مكافئي دوراني

انظر أيضًا

• سطح زائد
• سطح ناقص
• قطع مكافئ